Essential 3D math - Matrices

OpenGL uses matrix operations for a lot of purposes. For example, translations, scaling, rotations. Also computing of projection matrices, view matrices etc.

OpenGL uses 4x4 matrix used in homogenous coordinate system. Where each coordinate is represented as [x,y,z,w].Where w=1 for the affine transformations such as  translations, scaling, rotations. W can be any floating point number in the range -1.0 to 1.0 for projection matrices. During rasterization x, y, z coordinates are computed as  x/w, y/w and z/w. This is known as perspective divide.

OpenGL uses columnar matrix multiplication as shown below.

Identity Matrix

A special matrix having all elements along diagonal as 1 as shown below. 

It is associative, I*M = M*I = M. It's used in the computation of rotation, translation and scaling as discussed below.

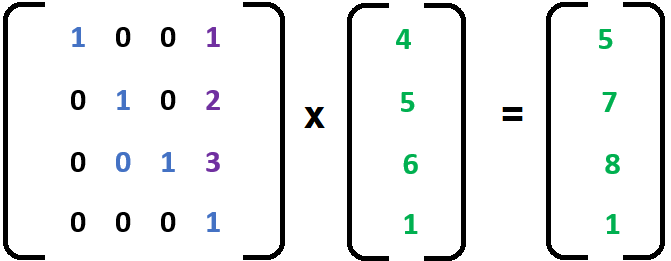
Translation Matrix

Translation matrix is used for moving around 3d objects.

Example:

Let's say there is a point [1,2,3] and want to translate by [4,5,6]. It can be accomplished as below. Resulting in  [5,7,9].

Scaling Matrix

Scaling matrix is used for Shrinking or Expanding 3d objects.

Example:

Let's say there is a point [1,2, 3] and want to  scale by [2,2,2]. It can be accomplished as below. Resulting in  [2,4,6].

Rotation

In 3D, rotation happens independently  on three cardinal axes X, Y, and Z.

Pitch or Rotation on X axis

The following matrix represents rotation matrix on X axis.

Example:

Let's say there is a point [1,2, 3] and want to  rotate by 90 degrees in X axis. It can be accomplished as below. Resulting in  [1,-3,2].

Yaw or Rotation on Y axis

The following matrix represents rotation matrix on Y axis.

Example:

Let's say there is a point [1,2, 3] and want to  rotate by 90 degrees in Y axis. It can be accomplished as below. Resulting in  [3,2,-1].

Roll or Rotation on Z  axis

The following matrix represents rotation matrix on Z axis.

Example:

Let's say there is a point [1,2, 3] and want to  rotate by 90 degrees in Z axis. It can be accomplished as below. Resulting in  [-2,1,3].

Essential 3D math - Vector

Following math concepts are essential for further understanding.

A 3D vector is represented as [Vx, Vy,  Vz] where  Vx, Vy and Vz represent numbers in 3D cartesian space. Vectors are attributed with a direction represented by its head  and a magnitude computed as square root of the squared sums of its components.

Unary negation and scalar multiplication 

The  negation and multiplication is done on all the components.

For example consider a vector

v=[1,2,3] so  2*v results in [2,4,6]. Similarly -v results in [-1,-2,-3].

Addition and Subtraction

Vectors can be added or subtracted. Here the individual components are added or subtracted. 

For example consider two vectors  A[1,2,3] and B[4,5,6]. 

A+B = [(1+4), (2+5), (3+6)] = [5, 7, 9].

A-B =  [(1-4), (2-5), (3-6)] = [-3, 3, -3].

Graphically represented as below, Note that the direction has changed  when arguments are reversed.

Unary Vectors

also known as normalized vectors are represented as V^{^}  have magnitude of 1. 

For Example V = [3,2,1]. It's normalized vector is calculated as

[2,3,1]/sqrt(4+9+1) = [3/3.74, 2/3.74, 1/3.74]=[0.8, 0.53, 0,27]

Dot Product

Dot Product of  two vectors is equal to the product of their magnitudes and the cosine of the angle between them. The notation used is a.b where a and b are vectors. It's mathematically represented as

a ·b = |a| x |b| x cos(θ).

It's graphically represented as 

To compute angle between two unit vectors, mathematically it can be represented as

The dot product may be a positive  or a negative or a zero.

Cross Product

Cross Product of  two vectors is equal to the product of their magnitudes and the sine of the angle between them. The notation used is axb where a and b are vectors.

Mathematically it's represented as

Cross product yields a vector that is perpendicular to the plane of two vectors a and b. Graphically it's represented as

The cross product of two vector is equal to area of their parallelogram.