Overview
vectors are widely used in 3D calculations. The following discusses it in detail.
Details
A 3D vector is represented as [Vx, Vy, Vz] where Vx, Vy and Vz represent numbers in 3D cartesian space. Vectors are attributed with a direction represented by its head and a magnitude computed as square root of the squared sums of its components.
Unary negation and scalar multiplication
The negation and multiplication is done on all the components.
For example consider a vector
v=[1,2,3] so 2*v results in [2,4,6]. Similarly -v results in [-1,-2,-3].
Addition and Subtraction
Vectors can be added or subtracted. Here the individual components are added or subtracted.
For example consider two vectors A[1,2,3] and B[4,5,6].
A+B = [(1+4), (2+5), (3+6)] = [5, 7, 9].
A-B = [(1-4), (2-5), (3-6)] = [-3, 3, -3].
Graphically represented as below, Note that the direction has changed when arguments are reversed.
Unary Vectors
Also known as normalized vectors are represented as V^ have magnitude of 1.
For Example V = [3,2,1]. It's normalized vector is calculated as
[2,3,1]/sqrt(4+9+1) = [3/3.74, 2/3.74, 1/3.74]=[0.8, 0.53, 0,27]
Dot Product
Dot Product of two vectors is equal to the product of their magnitudes and the cosine of the angle between them. The notation used is a.b where a and b are vectors. It's mathematically represented as
a ·b = |a| x |b| x cos(θ).
It's graphically represented as
To compute angle between two unit vectors, mathematically it can be represented as
The dot product may be a positive or a negative or a zero based on the direction of the vectors.
Cross Product
Cross Product of two vectors is equal to the product of their magnitudes and the sine of the angle between them. The notation used is axb where a and b are vectors.
Mathematically it's represented as
Cross product yields a vector that is perpendicular to the plane of two vectors a and b. Graphically it's represented as
The cross product of two vector is equal to area of their parallelogram.
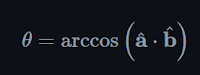
No comments:
Post a Comment