Understanding View space, Perspective and Orthographic Projections

So far our camera was in a fixed position and transformations happened in object space.  In this post we will  look at the larger picture.

As shown in the diagram below, a 3D object in a scene starts off from object space. Model transformation places it in the world space.  Based on the camera position the entire world is transformed into Camera space or view space. This is called view transform. This is done using viewing matrix. It is later moved to screen space using Projection matrix.

So far in our examples, camera is located at the origin and view and projection matrixes are not computed; instead identity matrix is used.  Next we will try to move around the camera and understand different type of projections.

Model Matrix

Model Matrix is responsible for moving 3D objects  from object space to world space. The affine transformation discussed in Lesson 06 are applied.

View Matrix

When the hypothetical camera position is changed, the whole world is transformed around it using view matrix. The view matrix is computed as below from glm as below.

mat4 lookAt(vec3 const& eye, vec3 const& center, vec3 const& up);

The internals is as described below (courtesy : learnopengl.com).

 

1. Camera position

The camera position or eye is a vector in world space that points to the camera's position. 

2. Camera direction vector

The  Camera direction vector is the direction at which the camera is pointing at. This is computed from the scene's origin or center in this case it's  (0,0,0). Subtracting the camera position vector from the scene's origin vector thus results in the direction vector. This must always point to +Z axis by RHS convention.

3. World up vector

The up vector (0,1,0) points to worlds Y axis. This may not be always the case.

4. Right axis vector

The right axis vector represents the positive x-axis of the camera space. This is obtained by doing a cross product on the up vector and the camera direction vector from step 2. 

5. Up axis vector

The Up axis vector points to camera's positive y-axis. It's computed by the cross product of the right and direction vector.

Output:

As mentioned earlier,  the World up vector need not be always (0,1,0).

For example,  if  the camera is moved on top of the cube say (0, 3, 0), we will be looking at the  top of the cube.  The eye is (0,3,0), center is (0,0.0) and up is (1, 0, 0) not (0,1,0).

Projections

The final matrix is projection matrix. There are two types of projections

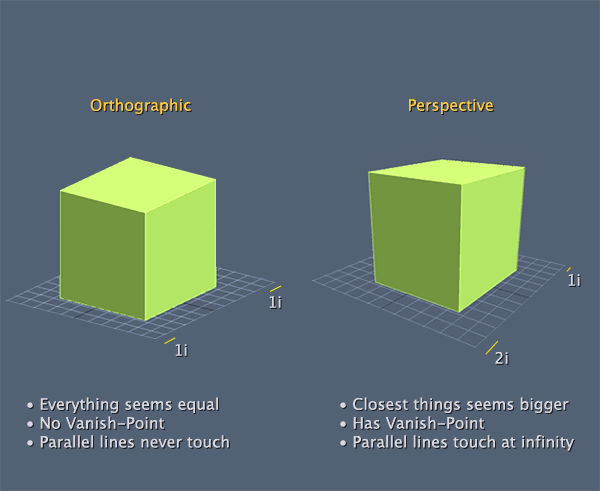
Orthographic and Perspective. The traits are as below.

The following shows another view with the view frustum. A view frustum is a rectangular box that confines the image rendered to be shown on the screen. 

The volume or the frustum is defined by the left, right, top, bottom, near and far plane values. 

The perspective projection is computed in glm as below

perspective(float fovy, float aspect, float zNear, float zFar);

In Perspective projection, the frustum appears as a truncated pyramid. 

fovy is the  Field of View (FOV) or zoom factor 

aspect is the aspect ratio of the viewport. i.e., width/height.

ZNear is the distance from the camera to the near plane

ZFar is the distance from the camera to the far plane

Example:

perspective(45.0, 1.84, 1.0, 100.0)

The screenshot below shows the perspective projection of the colored cube rotated 20 degree pitch and 20 degree yaw.

The ortho projection is computed in glm as below

ortho(xmin, xmax, ymin, ymax, zmin, zmax);

xmin, xmax are left and right of the view frustum

ymin, ymax are top and bottom of the view frustum

ZMin is the distance from the camera to the near plane

ZMax is the distance from the camera to the far plane

In orthogonal view it appears as a cube. 

Example: ortho(-1.84, 1.84, -1.0, 1.0, 1.0, 100.0); The 1.84 is the aspect ratio.

The screenshot below shows the orthographic  projection of the colored cube rotated 20 degree pitch and 20 degree yaw.

Unproject

Sometimes it's useful to x,y,z coordinates in the object space based on the mouse cursor position. UnProject() accomplishes this.  

The X,Y coordinates from the mouse cursor position and Z value from the depth buffer is used to compute the window coordinates. Later this is passed to glm unProject() along with Model, View and Projection Matrix, to get the co ordinates in world space.

For example, 

In the above, the red dot in the cube represents mouse cursor position  x = 353 y = 168

from depth buffer Z = 0.79

Using  Model, View, and Perspective Projection matrices, the world space coordinate is calculated as

0.22, 0.12, 0.43.